About the durability of Russian armor during the First World War
In this article, we will try to determine the durability of Russian armor of the First World War era. This question is extremely difficult, because it is extremely poorly covered in the literature. And the point is this.
It is well known that at the end of the XNUMXth century, the leading maritime powers in the construction of warships switched to armor made by the Krupp method. But this does not mean at all that since then the armor of the ships of all these countries has become equivalent.
The thing is that the "classic recipe" for Krupp's armor (also known as "quality 420", created in 1894) did not remain unchanged, but improved. At least by countries like England and Germany. But how exactly he perfected himself, and to what results the master armors of various powers came - this, alas, I do not know for certain.
Trial by fire
The projectile resistance of the Russian armor can be determined with acceptable accuracy, thanks to the experimental shelling of the old battleship "Chesma", reclassified as "excluded ship No. 4". An experimental compartment was created on the ship, copying the protection of various parts of the Sevastopol-class dreadnoughts, and for the purity of the experiment it was also equipped with many devices that such parts should have. So, for example, steam pipes (which passed there on battleships), shot guns, fire control devices and electrical wires, etc. were installed in the casemates.
Then the experimental compartment was shelled with various ammunition of caliber from 6 to 12 inches, including, of course, the latest 305-mm armor-piercing and high-explosive shells. That said, the test reports are very complete, as it should be in such cases. They contain not only a description of the consequences of a hit, but also the speed of the projectile at the moment it hits the armor, as well as the angle at which the projectile and armor meet.
All this makes it possible to calculate the resistance of Russian armor in relation to the latest domestic 470,9 kg shells, according to the same formula of Jacob de Marr, which I have already cited several times before. But I will cite it again, so that the dear reader does not have to ply through the previous articles. The ratio of the quality of the projectile and the durability of the armor in this formula is described by the coefficient "K". Moreover, the higher this coefficient, the stronger the armor.
A certain difficulty in assessing Russian armor is created by the fact that shells were tested primarily, and not the ultimate armor resistance of the protection of the latest dreadnoughts. It seems to be - what's the difference? But in fact, it is very significant. When projectiles are being tested, it is of interest to reliably hit armor at the main combat ranges. When the armor is tested, there is interest in the extreme conditions in which it can still protect the ship.
Nevertheless, the statistics of hits on the "excluded vessel No. 4" still allows us to draw certain conclusions.
About firing at 250 mm armor
Unfortunately, hits in armor from 125 mm or less are of no interest to us - in all cases it turned out that either the energy of the projectile was more than enough to penetrate it, or the angles of impact were so small that they gave a ricochet. In other words, statistics of hits on armor of 125 mm and below are useless to determine the durability of armor.
A different matter is hitting thick 225 mm and 250 mm armor, which we will consider in more detail.
Let's start with 250 mm of armor, which protected the walls of the conning tower of the "excluded ship No. 4". In total, 13 shots were fired at this wheelhouse, but some of them were fired at its roof, and others were high-explosive shells. Armor-piercing shells were fired at 250-mm armor only 5 times.
The most powerful shot was No. 6 (numbered according to test reports). A 305-mm armor-piercing projectile hit the armor plate at an angle of 80 ° (10 ° from the normal) at a speed of 557 m / s. The projectile would have a similar speed of 470,9 kg at a distance of only 45 cables. True, the angle of deviation from the normal would be less - 6,18 °.
Of course, the shell pierced the armor. To hold it, an armor with a "K" of more than 2 would be required. And this is an exorbitant value, even by the standards of the much more advanced armor of the Second World War. The calculations I made show that at a distance the Russian 700-mm / 305 gun mod. 52 could penetrate 1907 mm Krupp's armor plate "quality 433".
The remaining 4 shots were fired under equal conditions. The speed of the projectile on the armor was 457 m / s, the angles of encounter with the obstacle were about 80 ° (deviation from the normal 10 °). According to my calculations, Russian shells would have such a speed at a distance of 75 cables, but at the same time the angle of encounter with an obstacle would be worse - 76,1 ° (deviation from the normal - 13,89 °). In such conditions, according to the above calculations, 285,7 mm of Krupp armor penetrated (with K = 2000). But in reality everything turned out not so unambiguous.
During shot # 11, everything went smoothly. The armor-piercing one overcame the 250-mm armor plate, hit the opposite wall of the wheelhouse and already then exploded, making a pothole at the point of impact 100 mm deep. When shot # 10, the armor was also broken. But it is not entirely clear when exactly the shell burst occurred - this is not indicated in the report. But, apparently, this happened inside the conning tower, because the force of the explosion tore off the armor plates of the roof, and the adjacent 250-mm plate was simply ripped out of the mountings and deployed.
Thus, with this shot, the clear penetration and passage of the projectile should be counted for the armor protection as a whole.
But when shot # 9, there was a small incident - the shell hit the armor directly opposite the 70-mm floor. As a result, the 250-mm armor plate was pierced, and even its corner broke off, measuring about 450x600 mm, and a pothole 70 mm long was found in the 200-mm floor. Therefore, it can be argued that in this case, too, the projectile did not just pierce the armor, but did it with a decent amount of energy, which was enough to damage a horizontally located 70-mm armor steel sheet.
Accordingly, in four out of five hits, Russian armor-piercing shells showed quite the expected result, confirmed by calculations according to de Marr. But when shot # 7, a strange thing happened - the projectile hit the armor plate in exactly the same way, at the same 80 ° angle and with the same speed of 457 m / s, but did not pierce the armor, exploding during its passage. As a result, a pothole with a depth of 225-250 mm turned out: only "fragments of a shell weighing up to 16 kg."
We see that out of 4 hits of 305-mm armor-piercing shells, which should have penetrated armor over 285 mm thick, only 3 were “clean” penetrations. In one case, the shell exploded while passing through the armor, although it should not have been.
What is the reason for this fiasco? Perhaps it is the shell itself? Let us assume that a defective fuse has worked prematurely. But another interpretation is also possible: the fact is that the penetration of armor by a projectile is of a probabilistic nature. That is, there is no such thing that, for example, if, according to the Jacob de Marr formula, the maximum thickness of the armor pierced by a projectile under certain conditions is 285 mm, then the armor of 286 mm will not be penetrated by the projectile in any case. It may well break through. And vice versa - break under the same conditions against armor of a lesser thickness.
In other words, Jacob de Marr's formula itself (or any other analogous to it) does not at all have pharmaceutical accuracy. In reality, there are whole ranges in which a projectile hitting an armor plate at a certain angle and at a certain speed can penetrate the armor with a certain degree of probability, but this cannot be calculated using generally accepted armor penetration formulas. And it may well be that in the case of shot no. 7, the above-mentioned probability worked.
Thus, in my opinion, the results of shot # 7 are random and should not be taken into account. And the armor of Russian dreadnoughts with a thickness of 250 mm could not withstand the hit of 470,9 kg of a projectile at a speed of 457 m / s and an angle of encounter with an obstacle of about 80 °. According to de Marr, it turns out that the coefficient "K" of Russian armor in this case should be below 2. But how much?
In my opinion, the answer can be obtained by analyzing the consequences of shot no. 11. The round pierced a 250-mm plate, hit the opposite wall and made a 100-mm pothole there. Hence, we can assume that the maximum armor penetration of the Russian 470,9 kg projectile with the above parameters was 250 mm of Krupp's cemented armor. And an additional 100 mm of uncemented, homogeneous armor set apart.
Why is it homogeneous? The fact is that, as you know, cemented armor consists, as it were, of two layers. The upper one is very strong, but also fragile, and then softer, but also more viscous armor begins. The projectile, hitting the 250-mm armor plate, from the inside of the wheelhouse landed precisely in the "soft and viscous" layer, which in its qualities is more similar to homogeneous, rather than cemented armor.
In addition, you should take into account that I am calculating the "K" coefficient for a projectile that passes through the armor as a whole and explodes behind it. But in the case of shot No. 11, this is not what happened - the shell, breaking through 250 mm of Krupp's cemented armor and hitting the back side of the second plate, did not pierce the armor, but exploded, and only taking into account the energy of the explosion managed to make a 100-mm pothole. Thus, the calculation of "250 mm cemented + 100 mm homogeneous armor" can be considered made on assumptions that are obviously unfavorable for the armor. Accordingly, the result obtained can be considered the minimum below which the resistance of the Russian-made Krupp armor will not have.
And then the calculation is very simple. The speed of the projectile, as has been said many times above, is 457 m / s, the angle of deviation from the normal when it hits the 250 mm armor plate is 10 °. When this armor passes, the projectile will "turn" and hit the second plate already at an angle of 90 °, that is, 0 ° deviation from the normal. This follows from diagram No. 9 ““ Course of naval tactics. Artillery and Armor "L.G. Goncharov, given on page 132. Where, in addition to the strengths of the shells on impact, there is a graph of the turn of the shell when passing through the armor, depending on the angle of encounter with this armor.
The ratio of armor resistance of Russian homogeneous and cemented armor is unknown to me. But, according to G. Evers, the German cemented armor had a coefficient "K" 23% higher than homogeneous. And, probably, for the Russian armor, this ratio is also true. In addition, it should be noted that when passing through a 250-mm armor plate, the projectile will lose its armor-piercing cap. That, on the contrary, will lead to an increase in "K" homogeneous armor by 15%.
When calculating the speed of a projectile to penetrate a 100-mm homogeneous plate, the same formula was used as for a 250-mm cemented plate, only the "K" coefficient changed. I know that L.G. Goncharov recommended using a different formula for homogeneous armor, given in his own textbook. But she, according to him, is designed for armor plates thinner than 75 mm. We have, after all, 100 mm. In addition, according to G. Evers, the use of the above formula of Jacob de Marr is also applicable for homogeneous armor.
According to the results of calculating the "K" of cemented Russian armor, 2005 has a value. Now let's see if there were any cases during the shooting that refuted this result.
About firing at 225 mm armor
Only 225 rounds of armor-piercing shells were fired at 2-mm armor. Moreover, the speed of the projectile at the moment of contact with the armor was as much as 557 m / s - such a speed the projectile should have had at a distance of 45 cables. True, the angle of encounter with the armor was very unfavorable - 65 ° or 25 ° deviation from the normal. But even in this case, in order to withstand the impact of 470,9 kg of a projectile, the armor plate should have a coefficient "K" above 2 690. Which, of course, is completely impossible. In other words, when firing with such parameters, even the armor of the World War II era had to be pierced with a huge supply of energy from the projectile.
And with shot # 25, that's exactly how it happened. The shell easily pierced the 225-mm armor plate (it did not even break through, but simply broke a piece of 350x500 mm from it), then hit the bevel, which consisted of 25-mm armor on a 12-mm metal substrate, and made a 1x1,3 hole in it m. The exact location of the burst of the shell has not been established. But it was assumed that he went into the engine room and exploded already there. In other words, the result was exactly what one would expect with such a blow.
But with the second round (shot no. 27) everything turned out to be incomprehensible. The projectile deviated from the aiming point. And, as the report says, "hit the top edge of the armor." The result of the shot will be easier to quote from the document:

It is completely unclear what could have happened here. Primarily because it is not clear exactly where the shell hit. To begin with, “edge” is itself an extensible concept, since it can be used, among other things, to mean “the edge of something”. That is, it is even unclear whether the centerline of the projectile hit the vertical or horizontal surface of the armor plate.
But in the presence of a quality fuse, much more damage would be expected from any of these options. If the projectile hit the vertical plane of the armor, it should have collapsed to its full depth, not by 75 mm. If the impact fell on the horizontal part, then why did the report record the meeting angle of the obstacle of about 65 °? The projectile did not fall from the sky onto the horizontal surface of the 225-mm slab, it was fired at an angle of 65 ° to the vertical surface, which means that it should have been 25 ° relative to the horizontal. In this case, you can expect a rebound. Or (in case of a burst of a projectile) damage to the horizontal 225 mm armored deck adjacent to the upper edge of the 37,5-mm armor plate. But none of this happened.
In my opinion, the fault was a defective shell, which collapsed on impact, which is why the explosion was not at full strength. Or, perhaps, a defective fuse that detonated "high-explosive" at the moment the projectile touched the armor. It is also possible that the projectile was not defective, but collapsed because the angle formed by the two surfaces of the armor plate played the role of a kind of "cleaver". Formally, the projectile did not penetrate the 225 mm plates. But in connection with the extreme unusualness of the consequences of the hit, in my opinion, the reason should not be sought in the ultra-high qualities of the armor plate.
Consequently, the results of shelling the 225-mm armor plates of the "excluded vessel No. 4" do not confirm or refute our earlier conclusion.
However, there were other landmark tests of domestic shells and armor that took place in 1920. Here the goal was completely different. The experimental compartment was built under the Tsar-Father to determine the optimal protection scheme for future Russian dreadnoughts. But in 1917, the autocracy in Russia somehow went wrong. And projects for the construction of dreadnoughts have passed into the category of projecting. Nevertheless, the tests were carried out and including - using 305 mm 470,9 kg shells. The results are very interesting. But we will talk about this in the next article.
But what I would like to note separately is the presence of one glaring oddity in the tests. The fact is that they deliberately overestimated the distance of artillery fire.
So, for example, for shots at 225-mm armor with armor-piercing shells, it is indicated that the distance corresponding to the parameters of the shelling is 65 cables. But this is not true - at a speed of 557 m / s with a deviation from the normal of 25 °, a 305-mm projectile was supposed to penetrate the armor about 8% thicker than when firing at 65 cables, where the projectile speed would be 486,4 m, and the deflection from the normal - 10,91 °.
Of course, one can suspect a banal error in the calculations of the author of the article, that is, me. But how then to understand the firing at the conning tower - here in the documents the projectile speed is indicated all the same 557 m / s deviation from the normal - only 10 °, but the distance is considered the same, that is, 65 cables! In other words, it turns out that the "appropriate distance" was indicated at all without taking into account the angle of incidence, only by the speed of the projectile?
However, this version is easily verifiable. According to my calculations, the projectile speed for 60 cables is 502,8 m / s, and for 80 cables it is 444 m / s. At the same time, the data on the range firing of 305 mm / 52 guns, given by L.G. Goncharov ("Course of naval tactics. Artillery and armor", p. 35), show for these distances 1671 and 1481 ft / s, respectively, that is, translated into the metric system - 509 and 451 m / s.
Thus, we can assume that my calculator still gives a certain error downward, amounting to 6-7 m / s. But it is obvious that 557 m / s for 65 cables and 457 m / s for 83 cables are out of the question.
And one more fact that makes you think. As you can see, a total of 7 rounds of 305-mm armor-piercing shells were fired at 225-250 mm armor. At the same time, the shooting conditions were such that the specified armor had to break through with a considerable margin. Nevertheless, in real shooting conditions, even if at range, only in five cases out of seven shells pierced the armor. And only 4 shells passed inside.
Продолжение следует ...



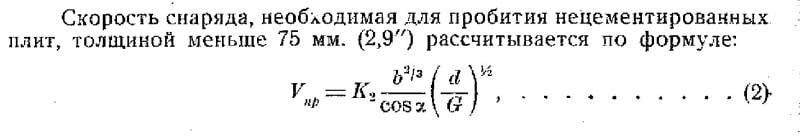

Information